Những bài toán về tam giác vuông thường sẽ liên quan trực tiếp đến các hệ thức nhất định. Do đó, để xác định được cách tính góc tam giác vuông nhanh nhất và chính xác nhất thì hãy tìm hiểu những hệ thức dưới đây. Hãy cùng keo nha cai w88 theo dõi và áp dụng đúng công thức để nhanh chóng giải quyết được các bài toán khó nhằn phía trước.
Hệ thức liên quan đến cạnh và đường cao trong tam giác vuông
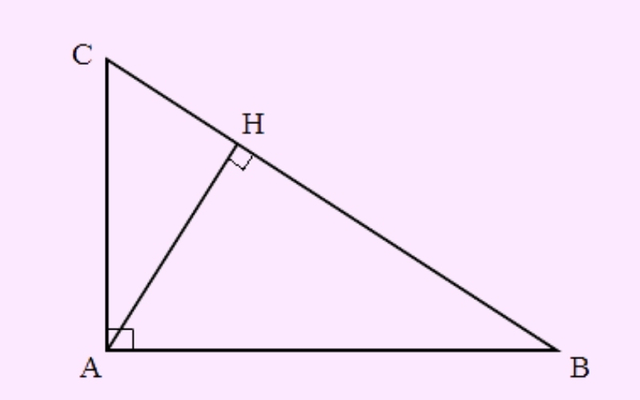
Trước tiên hãy cho tam giác được chọn là ΔABC với góc A là góc vuông và bằng 90 độ. Như vậy dựa theo ký hiệu AH ⊥ BC với cạnh góc vuông AB = c, AC = b, cạnh huyền BC = a và đường cao AH = h thì:
- BH = c’ (hình chiếu của AB xuống BC)
- CH = b’(hình chiếu của AC xuống BC)
Như vậy hệ thức được xác định sẽ là:
- c2 = a.c’ (tương ứng với AB2 = BH.BC)
- b2 = a.b’ (tương ứng với AC2 = CH.BC)
- h2 = b’.c’ (tương ứng với AH2 = CH.BH)
- b.c = a.h (tương ứng vớiAB.AC = AH.BC )
- 1/h2 = 1/b2 + 1/c2 (tương ứng với 1/AH2 = 1/AB2 + 1/AC2)
- b2 + c2 = a2 (tương ứng với AB2 + AC2 = BC2), dựa theo Định lý Pytago
Xem thêm >>> Học lỏm ngay Top 5 công thức tính chẵn lẻ xóc đĩa hiệu quả
Tỉ số lượng giác góc nhọn trong tam giác vuông
Tiếp theo đây sẽ là cách xác định tỷ số lượng giác góc nhọn và liên quan trực tiếp đến các cách tính góc tam giác vuông. Hãy đọc kỹ để xem xét định nghĩa và công thức được quy định sẵn.
Định nghĩa tỉ số lượng giác
Trong một tam giác vuông thì tỉ số lượng giác sẽ là:
- sinα = cạnh đối/ cạnh huyền
- cosα = cạnh kề/ cạnh huyền
- tanα = cạnh đối/ cạnh kề
- cotα = cạnh kề/ cạnh đối
Từ định nghĩa trên đây có thể rút ra được Định lí “ Trường hợp tam giác có hai góc phụ nhau thì sin góc này bằng cos góc kia, tương tự như vậy thì tang góc này bằng cotang góc kia” .
Một số hệ thức cơ bản và cách so sánh tỉ số lượng giác
Khi áp dụng định nghĩa cũng như định lý ở trên đây thì có thể rút ra được các hệ thức cơ bản dưới đây. Hãy chú ý đến hình ảnh về các hệ thức này để nắm được chính xác hơn cách tính góc tam giác vuông

Nếu cho α,β là hai góc nhọn trong một tam giác vuông và giả thiết rằng α < β thì có thể đưa ra được các kết luận dưới đây:
- Sinα < sinβ và tương tự thì tanα < tanβ
- Cosα > cosβ và tương tự thì cotα > cotβ
Các hệ thức về góc và cạnh có trong tam giác vuông
Tiếp theo sẽ là một vài thông tin liên quan đến các hệ thức về tam giác vuông. Những hệ thức này rất đơn giản và được quy định cụ thể như sau:
- Trong một tam giác vuông thì cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
- Trong một tam giác vuông thì cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề
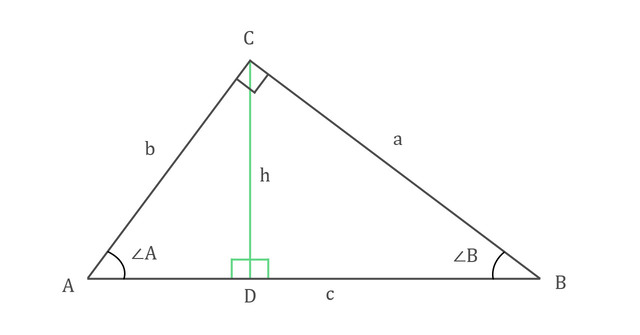
Lấy trường hợp tam giác ABC với quy định các cạnh đã nêu ở trên đây (AB = c, AC = b, cạnh huyền BC = a), từ đó khi tính cạnh tam giác thì công thức được sử dụng sẽ là:
- Cạnh b = a.sinB = a.cosC
- Cạnh c = a.sinC = a.cosB
- Cạnh b = c.tanB = c.cotC
- Cạnh c = b.tanB = b.cotC
Xem thêm >>> Dấu hiệu đề báo kép bằng ở giải đặc biệt chuẩn xác 100%
Áp dụng cách tính góc tam giác vuông trong các bài toán
Thông thường những đề toán liên quan đến tam giác vuông thường yêu cầu học sinh tính góc hoặc giá trị các cạnh cụ thể. Việc tính toán ở đây là một nhiệm vụ khá đơn giản, học sinh cần phải tìm ra được mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa được xác định. Tiếp theo đó là sử dụng các hệ thức về định lí cosin, định lí sin cũng như cách tính diện tích để có thể biết được giá trị của các yếu tố chưa được xác định mà bài toán yêu cầu.
- Giải tam giác vuông trường hợp đã biết một cạnh và hai góc: với những đề bài này thì hcoj sinh chỉ cần sử dụng định lí sin để tính cạnh còn lại
- Giải tam giác vuông trường hợp đã biết hai cạnh và góc xen giữa: các định lí cosin sẽ được dùng trong trường hợp này để tính cạnh thứ ba
- Giải tam giác vuông trường hợp đã biết khi biết ba cạnh: ở đây thì học sinh chỉ cần áp dụng định lí cosin để tính góc cụ thể là từ đó suy ra được giá trị của góc còn lại.
Khi giải các bài toán về tam giác vuông thì học sinh cũng cần linh hoạt và ghi nhớ các công thức thật chính xác. Từ những công thức tưởng chừng như rất đơn giản này lại có thể giúp hoá giải được các bài toán khó. Đặc biệt là việc tính giá trị các cạnh cũng như góc trong tam giác vuông sẽ trở nên nhanh chóng hơn rất nhiều.
Để tính góc tam giác vuông thì việc sử dụng các hệ thức trên đây chính là giải pháp hoàn hảo nhất. Học sinh có thể học thuộc các công thức và tỷ lệ lượng giác, tiếp theo đó là thực hành với các bài toán cơ bản. Khi đã nắm trong tay cược các công thức phù hợp thì hãy chuyển sang những bài toán phức tạp hơn. Tất nhiên sẽ có nhiều cách khác có thể hỗ trợ cho các bài toán hình, cụ thể là khi nói đến tam giác vuông, nếu muốn biết thêm thì hãy truy cập trang chủ của keo nha cai w88 ngay.


